Les Babyloniens ont suivi Jupiter grâce à des mathématiques géométriques sophistiquées
-
La géométrie utilisée fait allusion au calcul 1 500 ans avant les Européens.
Même lorsqu’une culture laisse derrière elle de nombreuses traces écrites, il peut être difficile de comprendre sa connaissance de la technologie et du monde naturel. Les documents écrits sont souvent partiels et les auteurs peuvent ignorer certaines technologies ou les considérer simplement comme banales. C’est pourquoi le monde antique peut encore offrir des surprises comme le mécanisme d’Anticythère, un ancien ordinateur mécanique qui mettait en valeur les connaissances des Grecs en mathématiques, en astronomie et en technologie mécanique nécessaire pour les relier.
Il a fallu plusieurs années après la découverte pour comprendre la véritable nature du mécanisme d’Anticythère. Et maintenant, quelque chose de similaire s’est produit pour les Babyloniens. Des tablettes d’argile, conservées au British Museum depuis des décennies, montrent que cette culture était capable d’utiliser une géométrie sophistiquée pour suivre l’orbite de Jupiter, en s’appuyant sur des méthodes qui, d’une certaine manière, préfigurent le développement du calcul des siècles plus tard.
Nous savions déjà que les Babyloniens suivaient les orbites de divers corps. Il existe environ 450 tablettes écrites décrivant les méthodes et les calculs que nous connaissons, et elles datent de 400 à 50 avant notre ère. La plupart de ceux qui décrivent comment calculer le mouvement orbital, selon les mots de Mathieu Ossendrijver de l’Université Humboldt, “peuvent être représentés sous forme d’organigrammes”. Selon la situation, ils décrivent une série d’additions, de soustractions et de multiplications qui pourraient vous indiquer où se trouverait un corps donné.
(Pour compliquer les choses, l’astronomie babylonienne fonctionnait en base 60, ce qui conduit à une notation très étrangère.)
Les Babyloniens avaient une compréhension des concepts géométriques – Ossendrijver les qualifie de « très courants dans le corpus mathématique babylonien » – mais aucun d’entre eux n’apparaissait dans leurs calculs astronomiques connus.
Au British Museum, cependant, il a trouvé une tablette qui n’avait pas été formellement décrite et qui contenait des parties de la procédure de suivi de Jupiter. Combiné avec d’autres tablettes, il commence avec le premier lever matinal de Jupiter, le suit à travers son apparent mouvement rétrograde et se termine par son dernier coucher visible au crépuscule. Encore une fois, c’est une question de procédure. Différentes sections sont utilisées pour prédire l’apparence de la planète sur différents segments de son orbite.
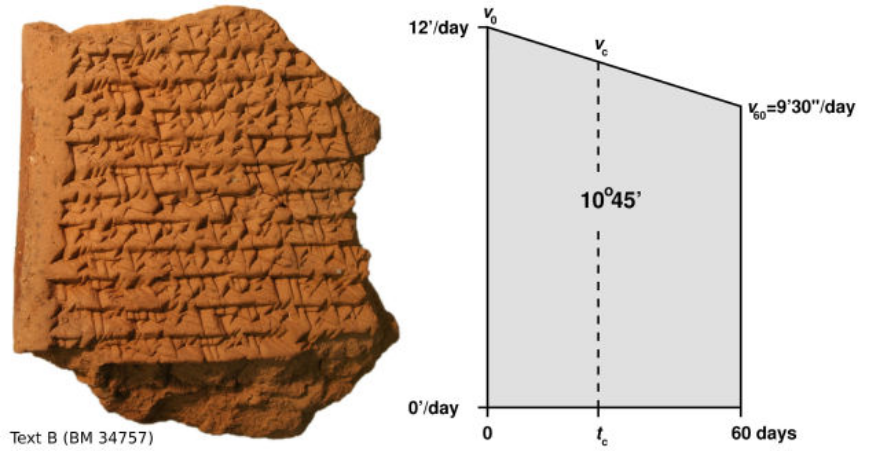
Ossendrijver a repris la procédure de calcul des 120 premiers jours et a montré que le calcul de son déplacement quotidien dans le temps produit un trapèze. Dans ce cas, la forme était en grande partie un rectangle mais avec sa face supérieure inclinée vers le bas au fil du temps en deux segments distincts. Une série d’autres tablettes traitaient explicitement les calculs comme produisant un trapèze.
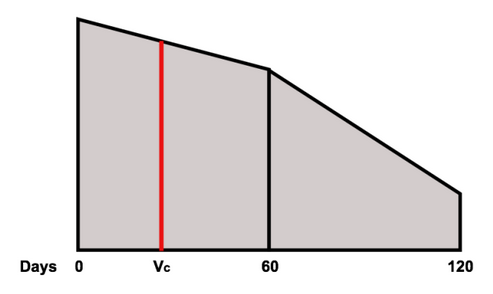
Le trapèze utilisé pour calculer les 120 premiers jours de l’orbite de Jupiter. La ligne rouge divise la première forme en deux zones égales.Les choses deviennent intéressantes dans la procédure suivante, qui est utilisée pour calculer le moment où Jupiter atteint le point médian dans la première moitié de cette étape de son mouvement. Cette procédure consistait à prendre la moitié gauche du trapèze et à la diviser en deux morceaux de surface égale. L’emplacement de la ligne de démarcation (étiquetée vc ci -dessus) produit alors la réponse. Comme le décrit Ossendrijver, “Ils ont calculé le moment où Jupiter parcourait la moitié de cette distance en divisant le trapèze en deux plus petits, de surface idéalement égale.”
Comprendre cela nécessitait évidemment une géométrie sophistiquée. Les érudits européens n’ont développé des méthodes similaires qu’au 14e siècle, lorsqu’elles ont été utilisées à Oxford. Les Grecs utilisaient la géométrie pour certains travaux astronomiques, mais cela impliquait des calculs de l’espace réel. Les Babyloniens travaillent ici dans un espace temps-vitesse abstrait.
Il est également frappant de constater que cette approche générale est similaire à certains aspects du calcul. Là, l’aire sous une courbe est calculée en créant mathématiquement un nombre infini de petites figures géométriques et en additionnant leurs aires. Rien n’indique que les Babyloniens étaient sur le point de faire ce saut intellectuel étant donné qu’ils n’ont divisé cette forme qu’à quelques reprises. Mais cela montre qu’ils ont reconnu la valeur de l’approche générale.
Hello! It looks like you're interested in this conversation, but you don't have an account yet.
Getting fed up of having to scroll through the same posts each visit? When you register for an account, you'll always come back to exactly where you were before, and choose to be notified of new replies (either via email, or push notification). You'll also be able to save bookmarks and upvote posts to show your appreciation to other community members.
With your input, this post could be even better 💗
S'inscrire Se connecter
